本篇文章是我C++更上一层楼的标志，也是我必须面对的一个知识点，那就是递归。

那么，递归到底是何方神圣？

递归递归，顾名思义

说起来递归，其实用中文理解起来很形象：传递、回归。

其实如果形象一点来说就是：自己调用自己，一个问题我分成多个问题去解。

那么递归到底该如何理解，我们来一个例子理解一下：

比方说我要计算n的阶乘，我们知道：

n! = 1 × 2 × 3 × 4 × …… × n

仔细观察一下，我们会发现：

3! = 1 × 2 × 3，但同时，3! = 2! × 3。

再观察一下其他数字，好像也是这样。也就是说，n!也等于(n - 1)!。

同时n-1的阶乘也可以以此类推，直到推到n = 1，1!就是1，那这样我们的思路就有了：

// The First Code
#include <bits/stdc++.h>
using namespace std;

int main() {
    int m = 1, n = 0;
    cin >> n;
    for (int i = 2; i <= n; ++i) {
        m = m * i;
    }
    cout << m;
    return 0;
}

验证下思路：输入数字n，也就是需要阶乘的数，但是我们定义了个m这个变量，这将每次的积给存在里面。

使用for循环，定义一个控制变量i，初始值赋为2，每一次都与m相乘，同时执行完一次循环后就自己加1，直到i = n，执行完最后一次循环后i > n，循环结束，输出阶乘数字。

但我们会发现这么做一点都不清晰，写循环的时候都要花个两年半，那么有没有更简单的操作？

我只想说：有的兄弟，有的，当然有，那就要请我们的递归老祖出山了。

上文中有提到：

仔细观察一下，我们会发现：

3! = 1 × 2 × 3，但同时，3! = 2! × 3。

再观察一下其他数字，好像也是这样。也就是说，n!也等于(n - 1)!。

这个思路不是闹着玩的，为什么我们不可以定义一个函数，然后自己调用自己？

于是，我们就会发现如果我们知道(n - 1)!的值，我们就可以知道n!，但这么以此类推，我们会发现怎么也绕不开1!，而1! = 1，把这些值带回去，我们会发现2! = 1 × 2，以此类推，最后算出n! = n × (n - 1)!的值。

令函数f(n)为n!，知道f(n - 1)，我们就可以求f(n)，同时f(n - 1)的求解过程和求f(n)的过程一模一样，我们就可以把这个问题分成这种子问题。直到f(1)，和俄罗斯套娃一样，我们在分析的时候会发现，n每次都在减1，同时每个阶乘都是从1开始乘，也就是必然都会经过f(1)这个数，所以这便是终止条件。

就比如求f(3)，那么f(3) = 3 × f(2)，f(2)本身就等于2 × f(1)，f(1)就等于1，然后就把1往回带，f(2) = 2 × f(1) = 2 × 1，f(3) = 3 × f(2) = 3 × 2 = 3 × 2 × 1，这个问题就这么解决了。

于是我们新定义的这个函数就可以这么写：

// 定义函数f()
int f(int n) {
    if (n == 1) {
        return 1;
    }
    return n * f(n - 1);
}

于是这个程序的代码就可以改成这样：

// The Second Code
#include <bits/stdc++.h>
using namespace std;

// 我们定义的递归函数f()
int f(int n) {
    // 终止条件
    if (n == 1) {
        return 1;
    }
    // 用递归解决n-1的问题
    return n * f(n - 1);
}

// 主函数
int main() {
    int n = 0;
    cin >> n;
    cout << f(n);     // 调用函数f()并输出f(n)的值
    return 0;
}

看似更复杂了，但这增加了程序的易读性，也让我们有更好的思路去解这一类题。

递归算法的总结

我们用递归解这一类问题的时候发现：递归将这个问题分解为多个子问题，除了数据不一样外，思路是一模一样的，是一类通过调用自身函数或方法的一种算法。

但是，递归算法必须明确一个递归的结束条件，不然就会存在栈溢出的情况。

总结一下上述我们程序的操作，不难发现可以整理成这个思路：

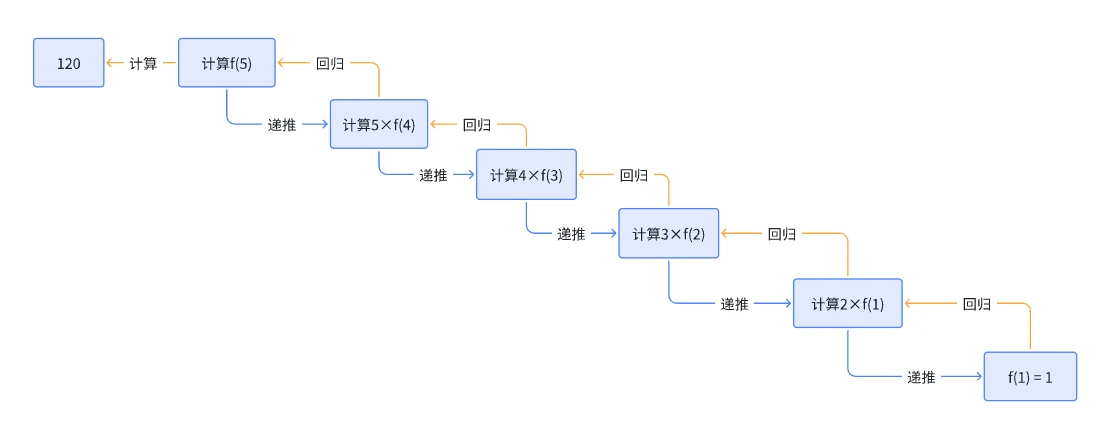
递推到最小值后便开始回归，并输出结果的值，由递推得到结果，这便是递归的基本逻辑。

为了加深递归这个概念，我们再举个例子：

递归算法的应用——斐波那契数列

斐波那契数列有一个特点，其数列的排列是：0，1，1，2，3，5，8，13，21，34，55……，我们先记这个数列为{a_n}，不难发现，从第三项开始，数列{a_n}里的数满足a_n = a_n-1 + a_n-2这个规律，我们定义：数列{a_n}中的数字称为斐波那契数。

输入一个正整数n表示第几项斐波那契数，令f(n)表示该数列的第n项，由第n项斐波那契数的规律，可以很轻松的得到第n项的斐波那契数递推式：f(n) = f(n - 1) + f(n - 2)

由于求f(n - 1)和f(n - 2)的过程与求f(n)的过程一模一样，我们就把他分成了n - 1和n - 2两个子问题开始求解，我们现在需要找一下这个数列的特殊之处：n每次都会减少1和2，所以就必会经过f(1)和f(2)两个斐波那契数，那么终止条件就写n = 1和n = 2两个，第一项为0就返回1，第二项为1就返回。

那么这个函数就很好定义了：

// 定义函数f()
int f(int n) {
    // 终止条件1
    if (n == 1) {
        return 0;
    }
    // 终止条件2
    if (n == 2) {
        return 1;
    }
    // 用递归解决n-1、n-2问题
    return f(n - 1) + f(n - 2);
}

代码写全便是：

// The Third Code
#include <bits/stdc++.h>
using namespace std;

// 定义函数f()
int f(int n) {
    // 终止条件1
    if (n == 1) {
        return 0;
    }
    // 终止条件2
    if (n == 2) {
        return 1;
    }
    // 用递归解决n-1、n-2问题
    return f(n - 1) + f(n - 2);
}

// 主函数
int main() {
    int n = 0;
    cin >> n;
    cout << f(n);   // 调用函数f()并输出f(n)的值
    return 0;
}

记忆化优化递归

接上一部分，我们随便取一个n的值，取5嘛，得：

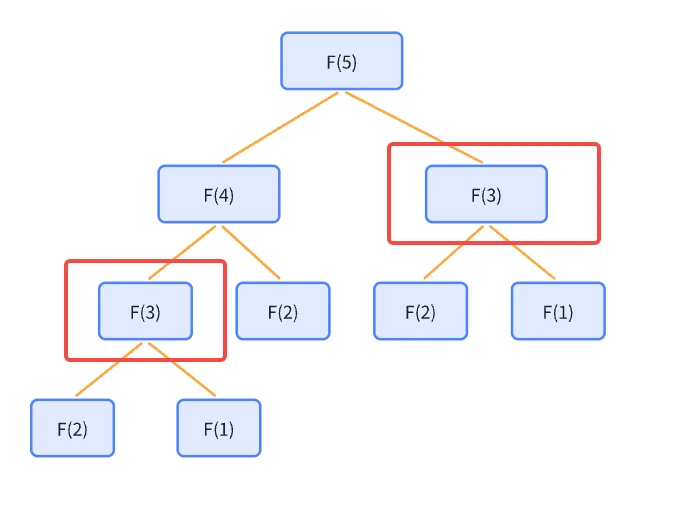
我们会发现，我们会重复计算f(3)这个部分，如果我们输入的n值够大，那么就还有更多的地方被重新计算，计算量就十分的大。

那我们要不这样：每次调用的时候，我们用数组将已经算了的结果先存起来，如果发现这个值计算过了，我们就直接使用计算结果不就行了嘛，这样就提高了程序执行的效率，减小了计算量。

这种优化的方法就叫记忆化。

优化一下这段函数：

// 定义函数f()
int f(int n) {
    if (a[n] > 0) {
        return a[n];    // 判断n是否被计算过，计算过那么返回即可
    }
    if (n == 1) {               
        return 0;       // 终止条件1
    }
    if (n == 2) {
        return 1;       // 终止条件2
    }
    // 返回并记录结果到一维数组a[n]中
    return a[n] = f(n - 1) + f(n - 2);
}

对了，记得定义一个数组，不然报错就没我事了。

最终代码

记忆化后，我们便得到了最终的代码：

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1000;
int a[maxn] = {};

// 定义函数f()
int f(int n) {
    if (a[n] > 0) {
        return a[n];    // 判断n是否被计算过，计算过那么返回即可
    }
    if (n == 1) {               
        return 0;       // 终止条件1
    }
    if (n == 2) {
        return 1;       // 终止条件2
    }
    // 返回并记录结果到一维数组a[n]中
    return a[n] = f(n - 1) + f(n - 2);
}

// 主函数
int main() {
    int n = 0;
    cin >> n;
    cout << f(n);   // 调用函数f()并输出f(n)的值
    return 0;
}

最后的最后

这篇文章应该是本博客中比较难消化的一篇，递归这个知识小改也消化了一点时间，说实话，的确比较难。

那么今天就先到这吧，晚安。