各位好,周末愉快,不过这个周好像要调休呜呜呜。
这个周也发生了很多事情,那让我们一一来讲。
英语周学情点评
这个周我们进行了英语的学情点评,不得不说十分不理想。
完型阅读各错2道,扣了7分,我以前基本都只扣1~2分的,这一次文章难度上来了,也翻了第一个车。
以及,语法填空错了一堆……
不过也算是开学后给我敲响的一次警钟吧,回归状态,找到以前做题的时候的感觉。
最后点评得分86/100,不理想,但我还会继续努力的,无限进步!
提前退役
没错,上个周我还去考CSP-J,才上了四节课左右,我就暂时退出竞赛班了。
说实话,我的进度其实也没差特别特别的多,但不过初三了,我也确实得重视学业了,毕竟要中考了。
与其说是班主任劝我退役,不如说是我自愿的,的确做了很久的心理斗争我才选择退出信息竞赛。
虽然心存遗憾,最后心里也的确做了很多斗争,后面也没撑住,还是哭了,但我认为我这个选择是正确的,以及,这也不代表我后面不能继续参加。
以及……我也想送给自己一句话:
当你有机会做出选择时,不要让自己后悔
无限进步!
备战学月学情点评
不知不觉就要一个月了,说实话,这一个月过的挺快的,我也将在国庆的时候迎来一次练习——9月学情点评。
据说这一次的学情点评后面会让学校参考学生的学业情况对教学进度进行合理调整,对我也挺重要的。
总之,这一次好好备战,无限进步!
Weather Situation
这几天的泸州天气挺有意思,一会儿下雨一会儿又不下雨,比较神秘。
不过万变不离其宗的是,每天早上都会下小雨。
然后就是,这几天真的凉快,我这几天坐在窗户旁边,一般情况下窗户开着的时候一阵风吹来真的很舒服。
几道有意思的题
暂时退出信息竞赛班后,我还是沉下来完成了几道今年泸州中考的题,其中有几道题也让我十分意犹未尽的,那么就分享一下吧~
2025泸州中考T10
已知抛物线$y=ax^2+bx+c$的对称轴为直线$x=-1$,与$y$轴的交点位于$x$轴下方,且$x=-1$时,$y>0$,下列结论正确的是
A.$2a=b$ B.$b^2-4ac<0$ C.$a-2b+4c<0$ D.$8a+c>0$
A选项很好排除,不难看出
$$
-\frac{b}{2a}=1 \Rightarrow 2a=-b
$$
这很显然与A矛盾,所以A错误。再看b选项,与$y$轴交点位于$x$轴下方,并且当$x=-1$时,$y>0$
如果按照这个要求画草图,你会发现这个抛物线他有如下特点:
- 开口朝上→$a>0$
- 与$x$轴有两个交点
所以这里的$\Delta=b^2-4ac$值应该是这样
$$
\Delta=b^2-4ac>0
$$
很显然,这里与B选项矛盾,也排除了。
C选项一时半会儿证不出来,先看D选项。
D选项这里,我们可以先令:$x=-1$,则有:
$$
\begin{equation} \left\{ \begin{array}{lr} a-b+c > 0 &\\ 2a=-b &\\ a > 0 \end{array} \right. \end{equation} \\\Rightarrow 3a+c>0 \Rightarrow 8a+c>0
$$
所以D是正确的。
至于C选项,我去找我们数学老师讨论了一下,尝试对C选项所给出的式子进行变形,然后消元:
$$
\begin{equation} \left\{ \begin{array}{lr} \frac{1}{4}a-\frac{1}{2}b+c<0 &\\ 2a=-b &\\ \end{array} \right. \end{equation} \\\Rightarrow \frac{5}{4}a-c<0
$$
很搞笑的一点是,你不知道$a$和$c$的关系,而且$x$在$-1$和$y$轴间,符号定不了,$C$选项就不一定正确。
所以这题选D,不过参考答案就很有意思了:

2025泸州中考T11
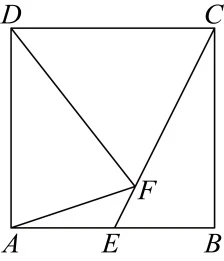
如图,在边长为$2$的正方形$ABCD$中,$E$为$AB$中点,$F$为$CE$上一点且$DF=DC$,则$AF$长为:
A.$\frac{2\sqrt{10}}{9}$ B.$\frac{2\sqrt{10}}{5}$ C.$\frac{4\sqrt{10}}{15}$ D.$\frac{4\sqrt{10}}{9}$
我第一次做这道题的时候是直接建系,但学了相似后,我就试了试用辅助线做这道题:过$F$点作$MN//AD$,设$EN=x$,因为$E$点是$AB$中点且正方形边长为$2$,所以$AE=BE=1$。
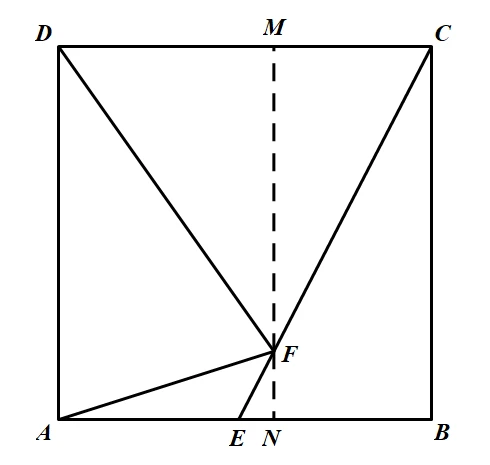
然后你会发现,这题瞪眼法都能瞪出$ΔBEC\backsimΔNEF$
这时候你会发现,$BE=1$,$BC=2$,由上,易证:
$$
\frac{EN}{EF}=\frac{BE}{BC}=\frac{1}{2} \Rightarrow NF=2x\\\Rightarrow MF=2-2x,DM=1+x,DF=DC=2
$$
看的出来,这里得用勾股定理:
$$
DM^2+MF^2=DF^2 \\\Rightarrow (1+x)^2+(2-2x)^2=4 \\\Rightarrow 5x^2-6x+1=0
$$
因式分解,得:
$$
(x-1)(5x-1)=0 \\\Rightarrow x_1=1, x_2=\frac{1}{5}
$$
很显然,$x$不能取$1$,所以$x = \frac{1}{5}$。
这个时候作$FP \perp AD$于点$P$:
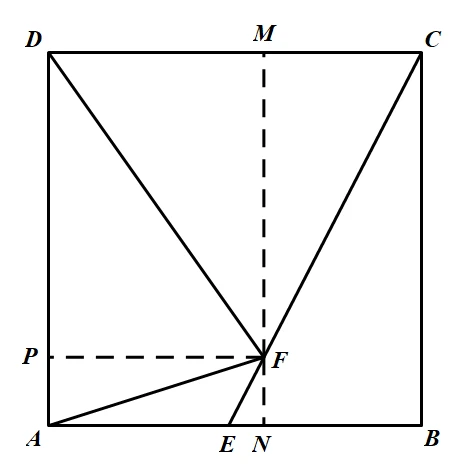
显然,你会发现把$x$带进去,然后就能求$DM$和$FN$,而$DM$又等于$PF$,$FN=PA$,这个时候又可以用一次勾股定理算$AF$:
$$
PF=DM=\frac{6}{5},FN=PA=\frac{2}{5} \\\Rightarrow AF=\sqrt{AP^2+FP^2}
$$
计算一下:
$$
AF=\sqrt{AP^2+FP^2}=\sqrt{(\frac{2}{5})^2 + (\frac{6}{5})^2}\\=\frac{\sqrt{40}}{5}=\frac{2\sqrt{10}}{5}
$$
最后求出
$$
AF=\frac{2\sqrt{10}}{5}
$$
故选B。
不过我很好奇,这题的出题老师是不是觉得自己很幽默,用这么多知识点,写这么一长串答案,到头来,不会的还不是建系,会的也想到了别的解法。

最后的话
不得不说,这个周发生的事情确实不少,也的确挫折挺多的,但毕竟也不能让这些影响到了我的心情。
初三就是这样,压力不小,挺过去就行了,总之就是拼搏一路赛到底嘛。
然后……就是犒劳自己辣~


最后,也祝自己月测加油,无限进步!



参与讨论