Hello, 欢迎来到我本年度42周记。

初三的活动谈不上有多么丰富，但至少每天过的还是相当充实，下面就请允许我分享本周的一些要事。

数学周测

这个周，十八班的人匆匆离场后老师便调了座位，并为我们做了思想工作。

做完思想工作后便是数学周测，虽然难度并不大，不过也仍然让我有些许意犹未尽，请允许我分享一下。

12/15/16

这三道题目，是我们这次周考25道题目中最难的3道。其中12题便是最难的。

我原先并不想理会这一道比较怪且长度比较长的新定义，结果当我做完压轴题后时间也才过了半个小时，但我看到12题所给出的方程有点诡异，似乎有点似曾相识，我立马尝试因式分解，结果还真可以。

不过踩坑的是，我没有想到这两根是不相等的实根，所以便痛失了这3分，不过我的思考方向是正确的。

第15题虽然难度并不小，但当我仔细品味15题后我才发现：

我在这道题目中发现了故人的影子

15.若 $a、b$ 是方程 $x^2+5x-7=0$ 的两个根，则代数式 $a^2+6a+b$ 的值是__.

这道题有一个难点，是你不知道这个 $6a$ 该如何处理。实际上，你会发现这个代数式可以做一个变形：

$$
a^2+6a+b=(a^2+5a)+(a+b)
$$

没错，前面一部分实在是太简单了，直接令 $x=a$，后把 $-7$ 移到右边去，就可以知道 $a^2+5a=7$ 了。$a+b$ 其实就是两根之和，使用韦达定理即可。

不过，在使用韦达定理前建议先验 $\Delta$，因为韦达定理的使用条件就是 $\Delta≥0$。

$$
\Delta=5^2+4×1×7=25+28=53>0
$$

很显然，这一题适用，于是：

$$
a+b=-\frac{b}{a}=-5
$$

所以

$$
a^2+6a+b\\=(a^2+5a)+(a+b)=7+(-5)=2
$$

所以这题的值便是2。

16题虽然类型的确是二次函数的代数压轴题，但由于比较常规，所以做起来还是很顺利的，不过由于时间原因和没考虑到对称轴，就没有想得很细致，这块地方又痛失3分。

还有4分在哪里

周测成绩下来了：108分，除了预料之外的6分以及答语写错的2分，我还被莫名其妙的扣了4分。

后面看了答题卡，发现分数扣在了反比例函数那里，但纳闷的是，我的解题没有任何毛病，答案也是对的，估计是改卷太快了没看清楚。

体训

上个月由于学校各种各样的安排，我们的体训一直都没有时间去妥善的处理，这一次周五下午，雨刚好停，我们便从这个周开始体训了。

虽然体训中的确很累，不过跑了几圈后很多烦恼都抛至脑后了，还是很轻松的。

分享两道题目

二次方程新定义

不是哥们，你这个新定义也不行啊，怎么因式分解一下就露出鸡脚了。

12.定义：已知 $x_1,x_2$ 是关于 $x$ 的一元二次方程 $ax^2+bx+c=0(a≠0)$ 的两个实数根，若 $x_1<x_2<0$，且 $1≤ \frac{x_1}{x_2} ≤3$ ，则称这个方程为 “友好方程“. 如：一元二次方程 $x^2+8x+15=0$ 的两根为 $x_1= -5$，$x_2=- 3$，且 $1≤ \frac{−5}{−3} ≤3$， 所以一元二次方程 $x^2+8x+15=0$ 为 “友好方程”．关于 $x$ 的一元二次方程 $x^2+(1-p)x-p=0$，有下列两个结论：

①当 $p=−\frac{4}{3}$ 时，该方程是 “友好方程”；

②若该方程是 “友好方程”，则有且仅有$3$个整数 $p$ 满足要求.

对于这两个结论，判断正确的是

A．①②都错误

B．①②都正确

C．①错误，②正确

D．①正确，②错误

这道题给出来的方程很有意思，不难看出这个方程可以被分解成以下形式，并且轻松得到两个根：

$$
(x-p)(x+1)=0 \Rightarrow x_1=p,x_2=-1
$$

那我们直接看结论①，$p=-\frac{4}{3}$ 显然不等于 $x_2$，并且我们可以也知道：

$$
1≤\frac{p}{-1}≤3\Rightarrow1≤\frac{4}{3}≤3
$$

这满足题目中关于 ”友好方程“ 的定义，所以结论①是正确的。

再看结论②，很显然可以得到一个解集得到 $p$ 的取值范围。

$$
1≤-p≤3 \Rightarrow -3 ≤ p ≤ -1
$$

并且，题目中也要求 $x_1 < x_2$，说白了就是 $x_1 ≠ x_2$，不去这个时候 $p$ 是整数，所以此时 $p=-2,-3$，有且只有两个整数 $p$ 满足要求，所以②错误。

故此题选D.

二次函数代数压轴

中考要是真这么考，我做梦都能被笑醒。

16.如图，抛物线$y=ax^2+bx+c$ 的对称轴为直线 $x=1$，与 x 轴分别交于 $(m,0)$，$(n,0)$，且 $m<n$．下列结论：①$a<0$；②直线 $y=2$ 与 $y=ax^2+bx+c$ 的交点个数为 1 个；③$at^2+bt>a+b(t≠1)$；④$m^2﹣2m=n^2﹣2n$．正确的有__（填序号）．

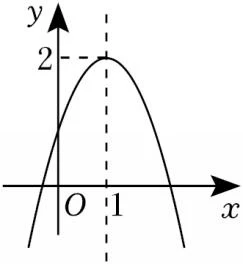
先看第一个结论，开口向下，$a<0$，送分的，①正确；看结论②，观察图像，抛物线顶点纵坐标为 $y=2$，的确这个抛物线与这条直线只有一个交点，②正确。

结论③看似陌如生，实际上你可以将这个式子处理成这个样子：

$$
at^2+bt+c>a+b+c(t≠1)
$$

这下你懂了不？

这样他的几何意义是这样：在函数 $f(x)=ax^2+bx+c$ 中，当函数值 $x=t$ 时，函数值 $f(t)=at^2+bt+c$；当函数值 $x=1$ 时，函数值 $f(1)=a+b+c$。

由图像可知，当 $x=1$ 时，$f(x)_{max}=f(1)=a+b+c$，说人话就是当 $x=1$ 时，函数取最大值，且 $t≠1$，所以这个结论应该是：

$$
at^2+bt+c<a+b+c(t≠1)
$$

不等号两边同时减 $c$，得：

$$
at^2+bt<a+b(t≠1)
$$

看一眼结论③，耶，不等号符号反嘞，故③错误。

结论④我上课的时候听了老师的方法，但我认为还是太麻烦了听完老师的方法后我尝试能否将其配成完全平方，于是我便对结论④两边同时加1，得到：

$$
m^2 -2m+1=n^2 -2n+1\\\Rightarrow (m-1)^2=(n-1)^2
$$

并且由题目可以知道：对称轴为直线 $x＝1$，且该抛物线与 $x$ 轴分别交于 $(m,0)$，$(n,0)$。这不很显然，这两个交点肯定关于对称轴对称，便易证：

$$
\frac{m+n}{2}=1\Rightarrow m+n=2
$$

这个恒等式可以帮助我们消元，我们就令 $n=2-m$ 把 $n$ 给消了，然后代入：

$$
(m-1)^2=(2-m-1)^2\\\Rightarrow (m-1)^2=(1-m)^2
$$

我们可以发现，括号内的值互为相反数，我们知道，互为相反数的两数平方的值相等，所以很显然，这是成立的，结论④是正确的。

如果对这个性质掌握不太熟的话，也可以通过完全平方公式 $(a±b)^2=a^2±2ab+b$ 进行展开，你会发现两边的值都是 $m^2-2m+1$，显然，结论④是正确的。

综上，这道题的答案便是：①②④.

学习班长

几个十八班的走后，由于我的成绩一直在班上都不错，所以便《顺理成章》的当上了班里的《学习班长》，虽然我上初三无意当任何班委，但还是被迫当上了。

不过，我这个人本身就很抽象，我还是很担心我当上学习班长后没几天这班风要被我糟蹋的差不多了（恼）

琐事&吐槽

刚接手学习班长，其实人还是很累的。毕竟班主任把很多不属于学习班长的职责划入到了学习班长的管辖范围之内，本来就初三了，我也并不完全自愿去接手这一职位，不过因为是同学选的，我也只能被迫接受。

刚上任学习班长便是一堆乱七八糟的事情，而且，作业板书本身也不是学习班长的任务，为什么要让我们去干这一件事？不是选了专员去板书作业的吗？

那也没办法咯，当我不知道班主任记忆不好吧

以及，为什么要在新的学期要求自习课整一个自习复习导向，有几个人会认真看吗？学的人早在课堂上学的很不错了，自己也知道要复习，不学的人永远都不会复习，那么这个复习导向到底是服务谁的？

没办法，班主任说中下游的学生自有人看，虽然我就是觉得他们也没几个人会去认真看

算了，反正事情过去了也罢，虽然确实要比以前学习班长的职位宽，但也不是不能办。

至少这并不影响我晚自习八点半前可以完成所有科目的作业

放学与放毒

走在回家的路上，这天气阴沉沉的，正如我出校门时的心情一样。

说到底，其实也不是我自己的怨气有多大，至少也是感受到的初三还是有强度的。

不过不得不吐槽的是，校内伙食是真的一言难尽，所以回家后……

结尾

这个周，谈不上发生了什么事，也谈不上心情有多么愉悦，可能也有初三正在慢慢起来的强度吧。

不过，至少每天过的还是相当充实，以及，我们最终也将会到达成功的彼岸。

保持热爱，共赴山海。无限进步，顶峰相见！