大家好，欢迎来到我本年度第43周的周记。

临近学校运动会，周记内容看似不多实际上每周已经开始忙到起飞了。

Weekly Keywords: 语文翻车，膝盖受伤，二次函数压轴，临近生日

语文翻车

语文翻车啊，不对劲啊，我解答题写得很好哇我觉得。
哦，原来我语文选择题错了五道啊，那没事了。

我们班里一直都有两大禁忌——一个是我的语文选择题，另一个是lmx同学的英语作业。

为什么都会被列为禁忌呢？因为错误率 真的高得离谱！

传说我当年语文选择题也是：

总共11道题，也就只错了10道题，喜提不及格。

不过这一次考试说实话，也的确没在状态，因为我带了点情绪去做题，这一点不予深究。

不过我也是天才，古诗词默写中有道题：

__________________，人迹板桥霜。

这道题是不是很正常，搞笑的是，我填的是 "凫雁满回塘"。

回家吧孩子，回家吧。

膝盖受伤

与其说是膝盖受伤，不如说是跑个1,000米时给我人跑虚脱了。

热身运动的时候我并没有特别认真的做，跑1,000米的时候刚跑200米我便有些许吃力了，虽然比起以前是有长进了

至少没有一跑完喉咙里全是血味道

但在最后50米冲刺的时候，我拼尽全力跑到终点，终于全班都进5分钟了，不过我的膝盖也受损了。

我寻思着之前跑1,000米为什么就没有这回事，偏偏这次跑后就会这样

二次函数压轴

“我知道你会来的。”
“为什么？”
“因为我们都太年轻，不知天高地厚。”

——from: 《哪吒之魔童脑海》

1.如图，在平面直角坐标系中，二次函数$y=ax^2+bx+c$交 $x$ 轴于点$A(-4,0)$，$B(2,0)$，交 $y$ 轴于点$C(0,6)$，在 $y$ 轴上有一点 $E(0,-2)$，连接$AE$. 抛物线对称轴上是否存在点$P$，使$\triangle{AEP}$为等腰三角形？若存在，请直接写出所有$P$点的坐标；若不存在，请说明理由．

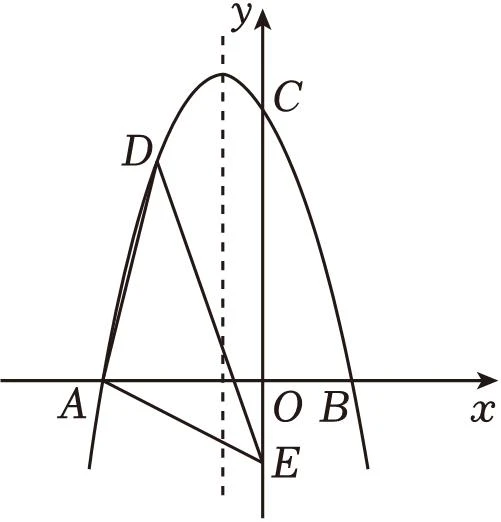
老师跟我们说过，二次函数的存在性问题不建议再使用几何法，可能会比较麻烦，但我做题的时候就不太信邪，便使用了几何法做题。

以两圆一线法画图，大概是这样：

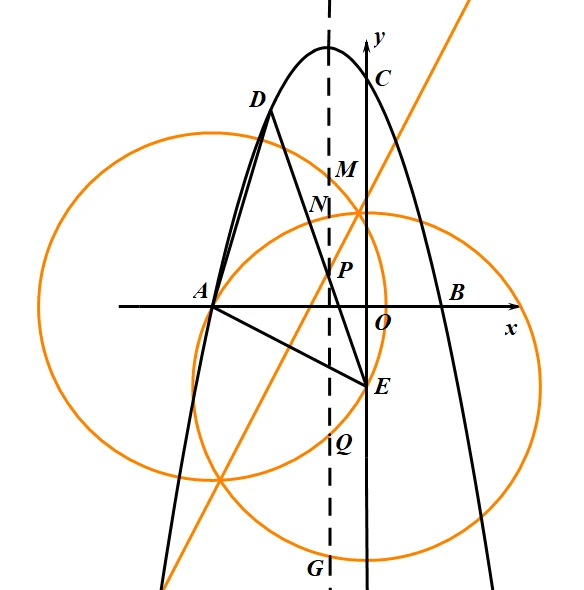
先分类讨论：以点$A$为圆心，$AE$为半径，看与对称轴的交点。第一个是$M$，也就是$P_1$，求出$AE$的长再用勾股算$P_1$到$x$轴的距离即可。

而再观察一下，这个圆与对称轴的另外一个交点便是$Q$，即$P_2$，取$P_1$纵坐标的相反数即可。

很容易求出这两点坐标：$P_1(-1,\sqrt{11})$，$P_2(-1,-\sqrt{11})$.

第二种情况，以点$E$为圆心，$EA$为半径，看与对称轴的交点。第一个是$N$，即$P_3$，然后再过点$E$往对称轴作垂线，交点为$F$，则此时用勾股算$NF$，然后你会发现$NF=GF$，且已知$E$点，我们就可以求出$P_3$和$P_4$（即$N$点了）

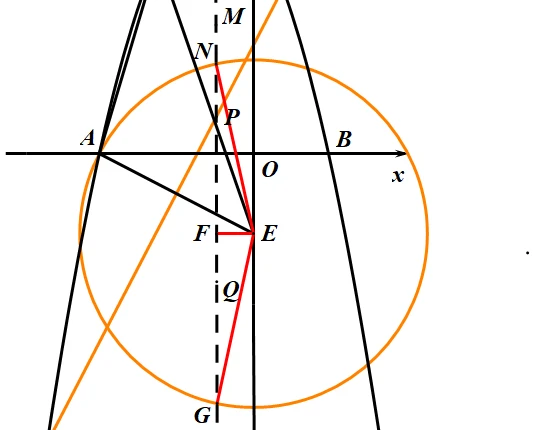
《经过一番简单的计算》，我们《轻而易举》的得出：
$$
P_3(-1,-2+\sqrt{19}),P_4(-1,-2-\sqrt{19})
$$
最后再研究P作为直角顶点的情况：

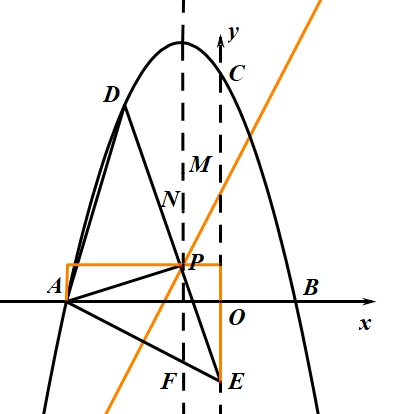
做出这个图就立马懂了，既然需要让$PA=PE$，那么让$|x_A-x_P|=|y_E-y_P|$，就行了。短边同理。

不过我认为，如果更严谨的话，那么可以设$P$点纵坐标，然后表示出$PA$和$PE$，算出来的结果应该是$P_5(-1,1)$

至此，这道题中的所有情况便这么做出来了。

至于为什么我要引用哪吒二的《不知天高地厚》的这一段话，其实也是说明有的时候没必要去装，的确，几何法真的有点麻烦，在一次函数存在性问题中都还行，但二次函数存在性问题的话，我认为还是盲算可能更友好点。

为何要选不知天高地后这一段话呢，因为我们数学老师说过在二次函数存在性问题中，尽量不要用几何法，但我偏偏不信邪。

生日将至

这么快就要15岁了吗，虽然不愿意承认，但时间也的确流逝的很快，我也在这几年中成长了很多。

从懵懂无知到即将面对中考，不禁感慨时间过得如此之快。

不过，我也要感谢陪伴我成长的家人、同学、朋友，他们都使我成长了许多……

以及……15岁生日时，也获得了一个很特别的生日礼物：

生日将至，提前祝我15岁生日快乐。

小的总结

不知不觉中，我也成长了不少。从以前懵懂无知的小学生，逐渐的开始成熟，以及，也即将踏上中考的征程。

这期间，我成长了不少，我感谢陪伴我的每一个人，即便这仅仅只是我生命中的一个过客，真没想到，时间会过的如此之快。

生日将至，提前祝我15岁生日快乐。

尘埃尚未落定，一切皆有可能。